Tensors of type 0/2

The product of two one- forms, written as defines a linear map which takes two vectors into the reals:

It is therefore a 0/2 tensor. denotes the   outer product. It is the formal notation to show how the 0/2 tensor is formed from two one- forms.

Note that this product is non- commutitative since gives a different result [ Assignment 3 ] i.e.

The most general 0/2 tensor is a linear sum of such outer products. So

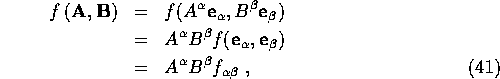
where are the components of the map f and we have used linearity.

If we take a basis  for f as [ 16 components ], then

But

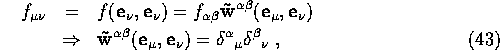
so we have

Under a Lorentz transformation  , the components of f become:

A 0/2 tensor is symmetric  if

and anti- symmetric  if

It follows that any 0/2 tensor can be uniquely decomposed into a symmetric  and anti- symmetric part .

with the symmetric and anti- symmetric parts given by

and